728x90
반응형
트리와 이진트리
트리(Tree)
계층적인 구조 표현
용어
트리는 노드(node)들과 노드들을 연결하는 링크(link) 로 구성됨
부모-자식 관계
- 루트노드를 제외한 모든 노드는 부모-자식 관계를 가짐
형제 관계
- 부모가 동일한 노드들
리프(leaf) 노드
- 자식이 없는 노드들
조상-자손 관계
- 부모-자식 관계를 확장한 것
부트리(subtree)
트리에서 어떤 한 노드와 그 노드의 자손들로 이루어진 트리
레벨
- 루트 노드부터 레벨 1 부터 부여된다 (0으로 시작할 수 있음)
높이
- 위 트리 높이는 4이다
트리의 기본적인 성질
- 노드가 N개인 트리는 항상 N-1개의 링크를 가진다
- 트리에서 루트에서 어떤 노드로 가는 경로는 유일하다. 또한 임의의 두 노드간의 경로도 유일하다. (같은 노드를 두 번 이상 방문하지 않는 다는 조건)
이진 트리 (Binary Tree)
- 이진 트리에서 각 노드는 최대 2개의 자식을 가진다.
- 각각의 자식 노드는 자신이 부모의 왼쪽 자식인지 오른쪽 자식인지가 지정된다. (자식이 한 명인 경우에도)
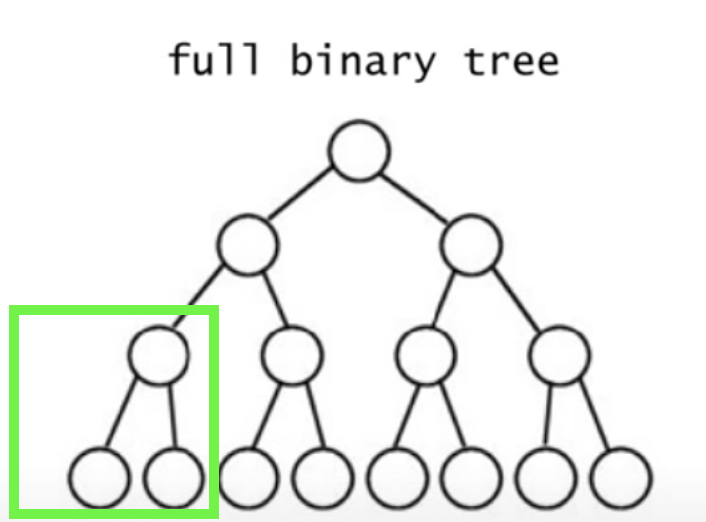
Full / Complete Binary Tree
Full Binary Tree : 모든 레벨에 노드들이 꽉 차있는 형태
Complete Binary Tree : 마지막 레벨을 제외하면 완전히 꽉 차있음, 마지막 레벨에는 가장 오른쪽부터 연속된 몇 개의 노드가 비어있을 수 있음
높이가 h인 full binary tree는 2^h-1개의 노드를 가진다.
노드가 N개인 full 혹은 complete 이진 트리의 높이는 O(logN)이다. (노드가 N개인 이진 트리의 높이는 최악의 경우 N이 될 수도 있다.)
이진 트리 표현
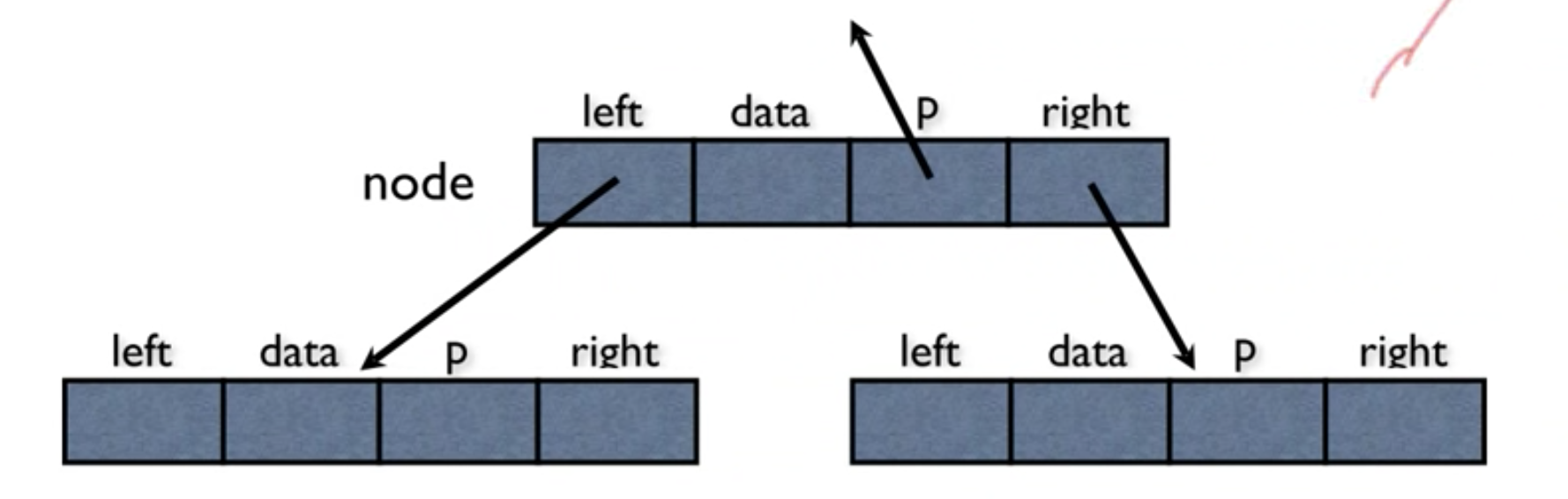
연결 구조로 표현 (Linked Structure)
각 노드에 하나의 데이터 필드와 왼쪽 자식(left), 오른쪽 자식(right), 부모 노드(p)의 주소를 저장 (부모 노드의 주소는 반드시 필요한 경우가 아니면 보통 생략)
이진 트리의 순화(traversal)
- 순회 : 이진 트리의 모든 노드를 방문하는 일
- 세 알고리즘은 매우 유사하다.
- 중순위(inorder) 순회
- 선순위(preorder) 순회
- 후순위(postorder) 순회
- level-order 순회
Inorder 순회
- 이진 트리를 루트 노드 r, 왼쪽 부트리 TL, 오른쪽 부트리 TR로 나누어 생각
- TL을 inorder로 순회
- r을 순회
- TR을 inorder로 순회
결과
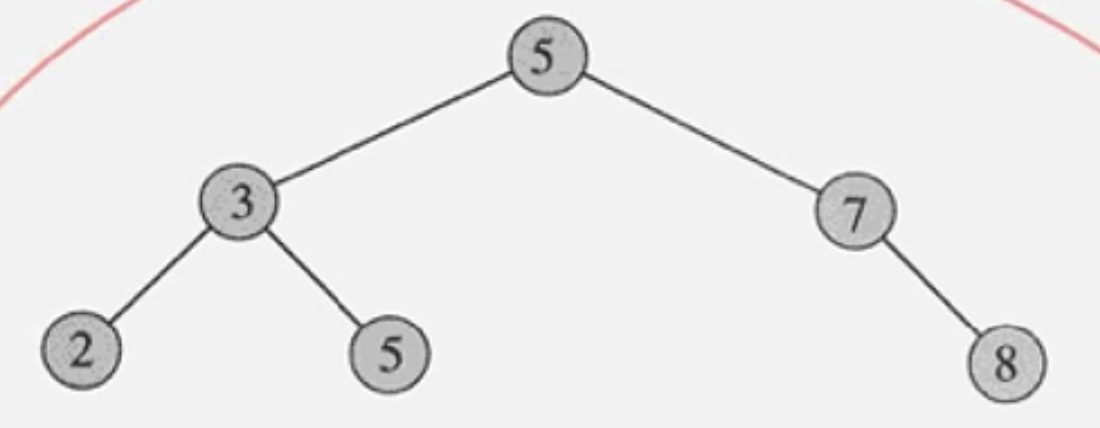
- 중순위 (inorder) : 2, 3, 5, 5, 7, 8 순으로 방문
- 선순위 (preorder) : 5, 3, 2, 5, 7, 8 순으로 방문
- 후순위 (postorder) : 2, 5, 3, 8, 7, 5 순으로 방문
반응형
'Programming > Algorithm' 카테고리의 다른 글
| [알고리즘] 6장 힙 정렬(Heap Sort) (0) | 2020.05.21 |
|---|---|
| [알고리즘] DFS & DFS (2) | 2020.04.06 |
| [알고리즘] 5강 빠른 정렬(Quick Sort) (0) | 2020.03.18 |
| [알고리즘] 4강 병합정렬 (merge sort) (0) | 2020.03.13 |
| [알고리즘] 3강 기본적인 정렬 알고리즘 정리 (0) | 2020.03.04 |